The Jones Polynomial
Table of Contents
The Kauffman Bracket
The Jones polynomial is a normalization of the Kauffman bracket that results in
a true knot invariant. The Kauffman bracket can be defined pictorially. If \(L\)
is a link diagram we define the Kauffman bracket recursively in terms of
smoothings of the crossings. The empty knot has bracket polynomial 1. Given
the disjoint union of a link \(L\) and an unknot \(S\) we define:
\begin{equation}
\langle{S\sqcup{L}}\rangle=(q+q^{-1})\langle{L}\rangle
\end{equation}
Lastly, the recursive step is given pictorially below.
This reduces an \(n\) crossing link to \(n-1\) crossings.

The smoothing on the left is called a zero-smoothing and right one is called
a one-smoothing.
This polynomial is invariant under Reidemeister II and III moves, but not I.
The recursive step can be expanded into a single sum. If we order the crossings
\(0\) to \(n-1\) we note that every integer between \(0\) and \(2^{n}-1\)
corresponds to a unique way of smoothing all of the crossings of the link
diagram. That is, write \(k\) in binary. If the \(m^{th}\) bit is \(0\) do a
zero-smoothing at the \(m^{th}\) crossing. Do a one-smoothing otherwise.
If we denote the number of disjoint cycles that result from this complete
smoothing by \(c(k)\) we obtain the following formula:
\begin{equation}
\langle{L}\rangle=\sum_{k=0}^{2^{n}-1}(-q)^{w(k)}(q+q^{-1})^{c(k)}
\end{equation}
where \(w(k)\) is the Hamming weight, the number of 1’s that occur in the
binary expansion of \(k\). With this it is evident that the formula
is exponential in the number of crossings, and is hence computationally
expensive. Recent algorithms have optimized this computation quite well, but it
is still a difficult calculation.
The Jones Polynomial
The Jones polynomial normalizes the Kauffman bracket by introducing a scale factor in terms of the writhe of the knot. The (unnormalized) Jones polynomial is given by: \begin{equation} J(L)=(-1)^{n_{-}}q^{n_{+}-n_{-}}\langle{L}\rangle \end{equation} where \(n_{\pm}\) are the number of positive and negative crossings in \(L\), respectively. The difference \(n_{+}-n_{-}\) is called the writhe of \(L\). With this normalization, the Jones polynomial is invariant under Reidemeister I moves, giving us a link invariant.
Sample Calculation
Let’s compute the Jones polynomial of the right-handed trefoil. Below we
draw the cube of resolutions for the knot. By invoking the sum above we can
calculate the Kauffman bracket of our diagram. We then normalize to obtain the
Jones polynomial.
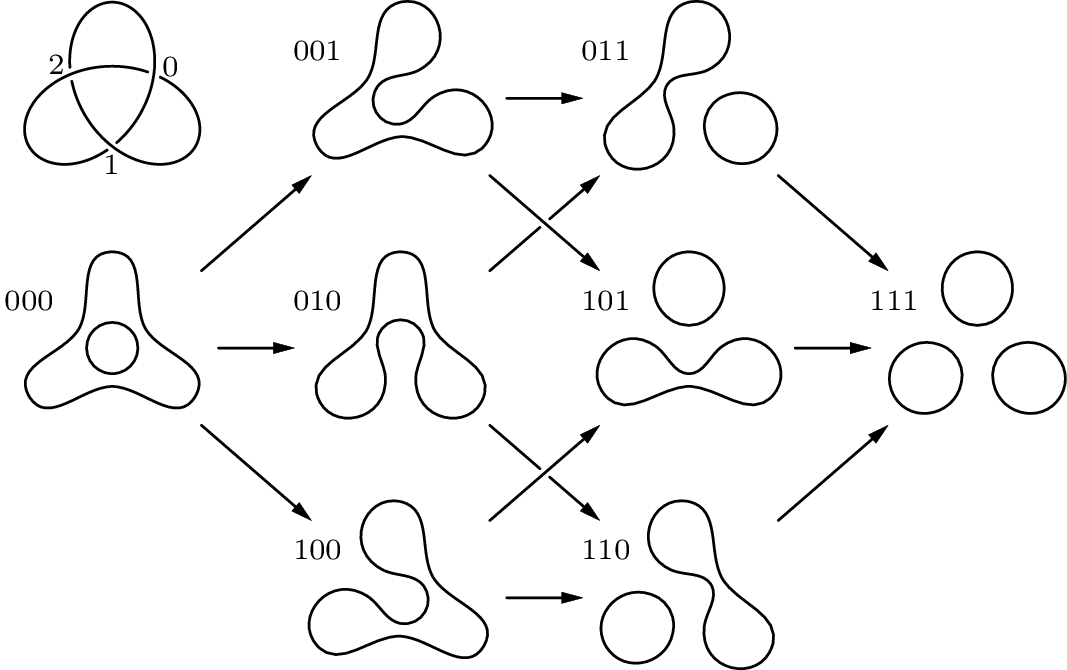
Since we have a 3 crossing knot, we must consider numbers between \(0\) and
\(7=2^{3}-1\). One number \((000_{2})\) yields Hamming weight 0, three
\((001_{2},\,010_{2},\,100_{2})\) have Hamming weight 1, three
\((011_{2},\,101_{2},\,110_{2})\) give Hamming weight 2, and one
\((111_{2})\) obtains Hamming weight 3. The picture above is drawn so that
the columns each have a constant Hamming weight, ordered left-to-right in
increasing order. All that is left to do is count the number of cycles in each
drawing. Fortunately, the smoothings yield identical cycle counts in a given
column. We can compute:
\begin{equation}
\langle{K}\rangle=\big((q+q^{-1})^{2}\big)-
\big(3q(q+q^{-1})\big)+
\big(3q^{2}(q+q^{-1})^{2}\big)-
\big(q^{3}(q+q^{-1})^{3}\big)
\end{equation}
The large parenthesis have been added to emphasize the groupings. Simplifying
we obtain:
\begin{equation}
\langle{K}\rangle=q^{-2}+1+q^{2}-q^{6}
\end{equation}
The right-handed trefoil has 3 positive crossings and 0 negative crossings.
The normalization factor is then \(q^{3}\). The final (unnormalized) Jones
polynomial is then:
\begin{equation}
J(K)=q+q^{3}+q^{5}-q^{9}
\end{equation}
Two common normalizations are found in the literature. Firstly one may note
that the Kauffman bracket of a non-empty link must be divisible by
\(q+q^{-1}\). One may wish to divide this factor out. In doing so we obtain
the normalized Jones polynomial. For the right-handed trefoil this is:
\begin{equation}
\tilde{J}(K)=q^{2}+q^{6}-q^{8}
\end{equation}
Lastly, many authors undertake the substitution \(q\mapsto{q}^{1/2}\). The
result is a Laurent polynomial in \(\sqrt{q}\). This final version of the
Jones polynomial yields the following equation for the right-handed trefoil:
\begin{equation}
\hat{J}(K)=q+q^{3}-q^{4}
\end{equation}
Data Sets
The Jones polynomials of all knots with up to 19 crossings have been tabulated below. If you do not care about the type of knots and just want as much data as possible, download the all_jones.tar.xz file.